問題解決にあたってのモデルのご紹介です。理科の授業や目標達成への活動、生徒会活動などで使えるかと思います。ただ、このモデルが絶対正しい、他にモデルはないという訳ではなく、取り組む問題や立場、場面などによって違うと思います。問題解決モデルの一つとしてご参考ください。
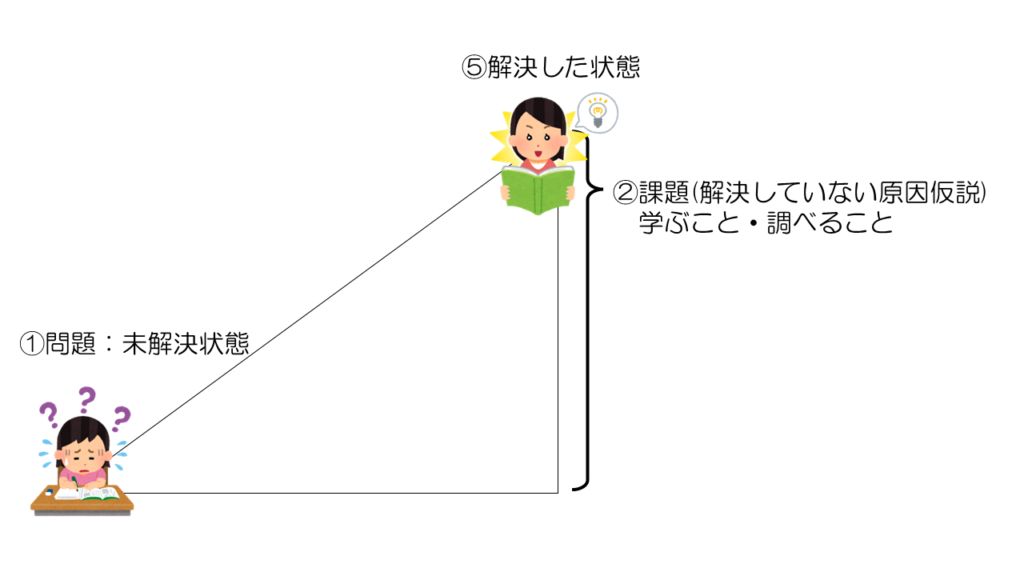
まず、図1の説明です。直角三角形の左下が未解決の問題を発見した状態①になります。そして、右上が問題を解決した状態⑤になります。そして、⑤の状態になりたいんだけど、①になってしまっている原因の仮説が課題②です。※仮説とは根拠のある予想です。
別の言い方をすると、適切に課題を設定してクリアする(学んだり、調べたりする)ことができれば、⑤になれない原因をつぶすことになるので、①から⑤に状態が変わるということです。ただし、②はあくまでも課題の仮説なので、実際に行動してみないと正しい課題なのかが分かりません。この②課題を設定できるか?が最も大切ですが、授業では教員が設定することが多いため、なかなか磨けない力になります。
例えば、①植物の分類ができない人が、⑤できるようになりたいと思ったときに、②には、そもそもの分類方法を学ばなければいけない人もいれば、植物の特徴を学ばなければいけない人もいます。このように人によって課題は違うので、自分で設定できないと、できるようにならないのです。教師が40名の生徒一人一人に設定するのは現実的に無理なのです。だからこそ、自分で課題を設定する力は重要なのです。
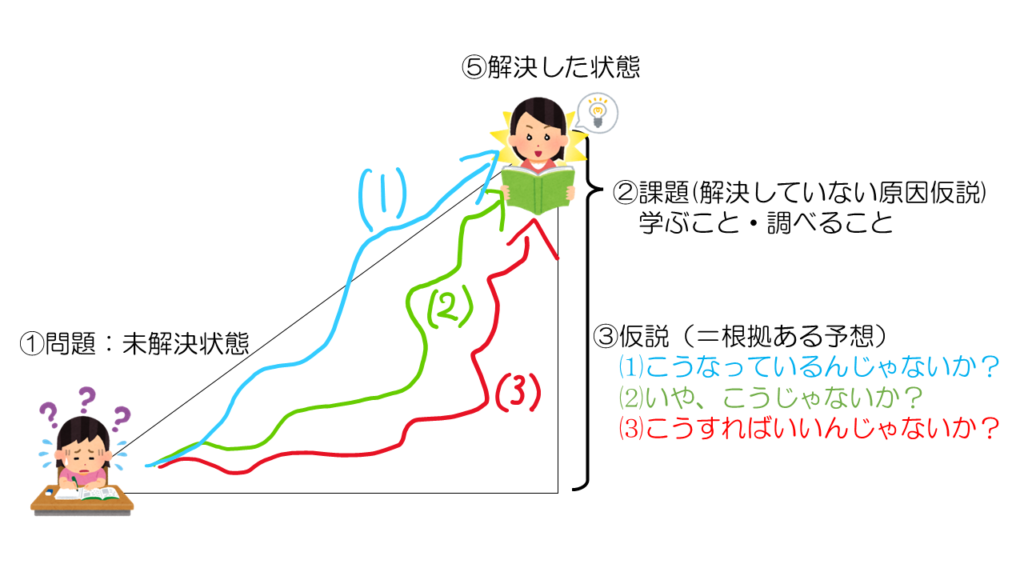
課題②を設定したら次は、こうなっているんじゃないか?こうすればいいんじゃないか?の仮説③を立てます。三角形で言うと、①から⑤の状態になるために、どのようなルートを上るか?というのが仮説になります。この仮説が間違っていると、当然ですが⑤まで登れません。別の仮説を試すか、もう一度課題を設定し直すかなどの試行錯誤になります。
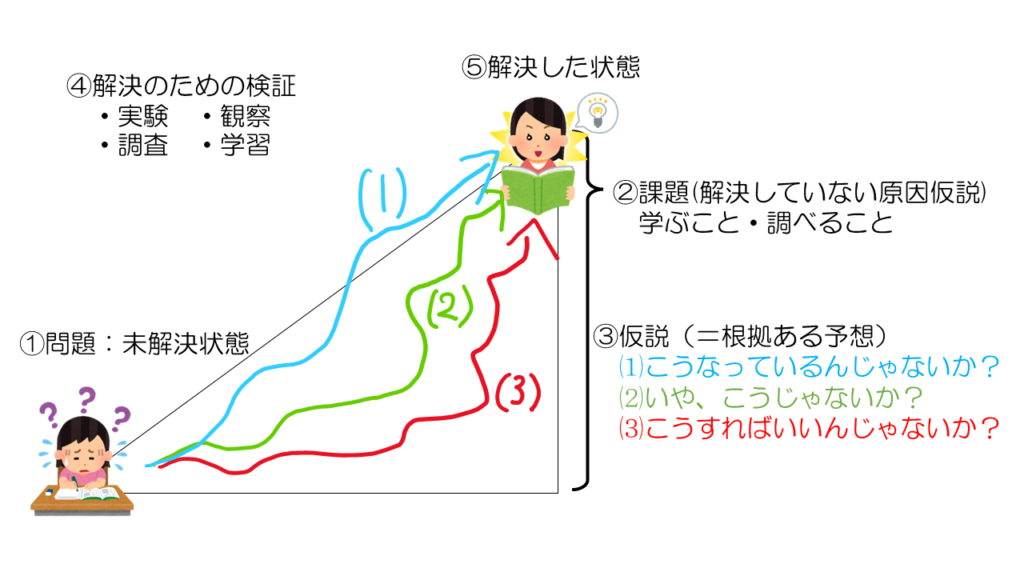
そして、仮説が合っているか?の検証をするために実験や観察、調査、学習を行うのが④です。自分の立てた仮説⑴~⑶に対して実験や観察、調査、学習などの方法を使って⑤まで登れるかを検証するのです。解決できれば②課題と③仮説が正しいことが証明されます。また、⑤に到達します。このようにして理科の問題解決が進んでいきいます。
ただし、これを実行するには判断力が必要です。例えば、設定した課題は適切なのか?立てた仮説は正しそうなのか?仮説の検証にはこの実験でよいのだろうか?などです。多くの人が、この判断をできません。理由は、判断する経験が圧倒的に不足しているからです。友達や先生の力を借りて判断する経験をしていき、たくさんの失敗をしながら自分で判断できるようにしていくことも理科で問題解決に取り組む目的の一つと考えています。
問題解決に取り組むのは自分ですが、いろいろな人の力を借りて達成していきましょう。その過程で、あなた自身の力が育まれていくと信じています。まずはやってみよう!
ちなみに僕の授業動画は問題解決の流れに沿って進みます(下記参照)。自分の判断を友達や先生に相談しつつ問題解決をしていける環境(まさに授業中が最適)があれば、問題解決に関する力や判断する力を身に付けることができるのではないでしょうか。